رابطه بازگشتی

          حامد شیرزاد 
            بازدید : 861
          پنجشنبه 03 آذر 1390
           نظرات (0)
        

رابطهٔ بازگشتی، در ریاضیات، دنباله‌ای است که به صورت بازگشتی تعریف می‌شود.

معادلهٔ تفاضلی نوع خاصی از رابطهٔ بازگشتی است.

بسیاری از روابط بازگشتی ممکن است رفتارهای پیچیده‌ای از خودشان نشان دهند این نوع روابط توسط فیزیکدانان و ریاضیدانان در شاخه‌ای از ریاضیات به نام انالیز غیر خطی مطالعه می‌شوند. حل یک معادله معادله بازگشتی یعنی به دست اوردن یک فرم بسته برای ان (یک تابع غیر بازگشتی از n ).

محتویات

[نهفتن]

رابطهٔ بازگشتی خطی همگن با ضرایب ثابت [ویرایش]

اصطلاح خطی به این معناست که هر جمله‌ای این توالی به صورت یک تابع خطی از جمله‌های قبلی تعریف می‌شود. مرتبهٔ یک رابطهٔ بازگشتی خطی برابراست با تعداد جمله‌های قبلی مورد نیاز توسط تعریف. به عنوان مثال $a n = a n - 2$ از مرتبهٔ 2 است.زیرا حتماً باید جملهٔ قبل وجود داشته باشند(چه هر دو استفاده شوند، چه نشوند)

فرم کلی رابطهٔ بازگشتی خطی همگن از مرتبهٔ d: : $a_n = c_1a_{n-1} + c_2a_{n-2}+\cdots+c_da_{n-d} + c \,$

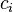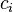$c \,$ و $c_i \,$ می‌توانند به n وابسته باشند اما $a_i \,$ ها نه. اگر تمام $c_i \,$ ها مستقل از n باشند گفته می‌شود این رابطه دارای ضرایب ثابت است، همچنین اگر $c = 0 \,$ گفته می‌شود که رابطهٔ بازگشتی خطی است که گاهی LRS نیز گفته می‌شود.

رابطهٔ بازگشتی خطی با مقادیر اولیهٔ (شرایط اولیه) $a_0,\dots,a_{d-1}$ یک توالی یکتا را مشخص می‌کند.

مثال:اعداد فیبوناچی [ویرایش]

اعداد فیبوناچی به صورت رابطه بازگشتی خطی تعریف می‌شوند: 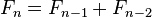$F_{n} = F_{n-1}+F_{n-2} \,$ با مقادیر اولیهٔ : $F_1 = 1 \,$ و: $F_2 = 1. \,$ دنبالهٔ اعداد فیبوناچی ...۱,1,2,3,5,8 این دنباله را می‌توان با راه حل ماتریسی که در زیر شرح داده می‌شود حل کرد.

حل کردن توسط جبر خطی [ویرایش]

با داشتن یک رابطهٔ بازگشتی خطی می‌توان ماتریسی برای ان نوشت : $\begin{bmatrix}a_0\\ \vdots\\ a_{d-1}\end{bmatrix} = b_1v_1 + \cdots + b_dv_d$

$\begin{bmatrix}a_n\\ \vdots\\ a_{n+(d-1)}\end{bmatrix} = C^n\begin{bmatrix}a_0\\ \vdots\\ a_{d-1}\end{bmatrix} = C^n(b_1v_1 + \cdots + b_dv_d) = \lambda_1^nb_1v_1 + \cdots + \lambda_d^n b_dv_d$

پس فرم بسته $a n$ بدست امد.

حل کردن به صورت عمومی [ویرایش]

راه حل‌ها برای رابطهٔ بازگشتی اصولی با قاعده هستند . اغلب با تابع مولد یا با توجه به این کهrⁿ یک جواب برای مقادیر ویژه r است.رابطهٔ باز گشتی زیر را در نظر بگیرید: $a_{n}=Aa_{n-1}+Ba_{n-2}. \,$ فرض کنید جواب ان به فرم a_n = rⁿ است . در نتیجه : $r^{n}=Ar^{n-1}+Br^{n-2}. \,$ با تقسیم بر r^n − 2

$r^2=Ar+B, \,$

$r^2-Ar-B=0. \,$

به این معادله، معادله مشخصهٔ رابطه بازگشتی گفته می‌شود با حل این معادله دو مقدار برایr، بدست می اید که اگر متمایز باشند جواب عبارتست از :

$a_n = C\lambda_1^n+D\lambda_2^n \,$

اما اگر λ₁, λ₂ برابر باشند جواب عبارتست از :

$a_n = C\lambda^n+Dn\lambda^n \,$

CوD با مقادیر اولیه a₀ = a, a₁ = b مشخص می‌شوند.

برچسب ها رابطه بازگشتی ,

ارسال نظر برای این مطلب

عنوان	پاسخ	بازدید	توسط
دانلود جزوه ی سیستم عامل پیشرفته استاد برومند نیا	0	2854	admin
دانلود نمونه سوالات درس طراحی الگوریتم پیشرفته	0	1716	admin
دانلود نمونه سوالات درس سیستم عامل پیشرفته	0	3762	admin
دانلود جزوه سیستم عامل پیشرفته - استاد زیاری	0	2073	admin
اسلاید های درس سیستم عامل پیشرفته :: دکتر برومند نیا	0	1863	admin